中文题目：基于改进高斯聚类算法的原油采购与调和集成优化加速求解方法

论文题目：An Improved Gaussian Clustering Algorithm to Accelerate the Solving of Integrated Optimization of Crude Oil Procurement and Blending

录用期刊/会议： Industrial & Engineering Chemistry Research (中科院大类3区，CAA B类期刊)

原文DOI：http://doi.org/10.1021/acs.iecr.4c03924

原文链接：http://pubs.acs.org/doi/full/10.1021/acs.iecr.4c03924

录用/见刊时间：2025年3月18日

作者列表：

1）郑万鹏 中国天天色天天（北京）自动化系 博19

2）高小永 中国天天色天天（北京）自动化系 教师

3）潘   辉 中国石油独山子石化分公司

4）左   信 中国天天色天天（北京）自动化系 教师

5）黄德先 清华大学自动化系 教师

6）张歆瞳 中国天天色天天（北京）自动化系 博22

7）黄付宇 中国天天色天天（北京）自动化系 硕20

文章简介:

本文提出了一种改进的高斯混合模型（GMM）算法，用于加速原油采购与调和集成优化问题的求解。针对原油采购与调和过程中原油种类过多导致模型难以求解的问题，文章通过引入改进的GMM算法进行原油预筛选，有效缩小了搜索空间，从而显著提高了求解效率。

摘要:

原油采购与调和工艺是炼油企业生产运营的核心环节，其集成优化对保障调和油性质稳定至关重要。然而，当候选原油种类过多时，集成模型将变得难以甚至无法求解。针对这一问题，本文提出一种改进的高斯聚类算法，通过预先筛选合适的原油参与集成优化，从而大幅压缩求解空间并提升计算效率。首先，本文详细介绍了用于原油聚类的改进GMM算法，并提出了带有价格补偿函数的期望最大化（EM）算法，以减少原油价格波动对聚类结果的影响。随后，通过实际案例和对比实验验证了改进GMM算法的有效性。结果显示，改进后的GMM算法将求解时间缩短了约90%。改进后的GMM算法可以显著提高求解效率，而带有价格补偿函数的EM算法则能有效降低原油价格波动对聚类结果的影响。最后，本文提出的基于原油预选的优化方法为现场应用奠定了基础并提供了可能性。

背景与动机:

炼油企业的原油采购与调和过程是生产和运营的核心环节，其集成优化对于保证调和油性质的稳定具有至关重要的意义。随着全球原油市场的日益复杂和多样化，炼油企业面临着越来越多的原油选择。然而，候选原油种类的增加给集成优化模型的求解带来了巨大的挑战。一方面，原油的性质差异显著，包括硫含量、氮含量、重金属含量、收率等多个维度，这些因素都直接影响着原油的调和效果和炼油过程的经济性。另一方面，传统的优化算法在处理大规模变量和约束时，往往计算复杂度高，求解效率低，难以满足实际生产的需求。

在此背景下，本文提出了基于改进高斯聚类算法的原油预选方法，旨在通过预先筛选出合适的原油种类，大幅度缩小集成优化模型的搜索空间，从而提高求解效率。这一方法的提出，不仅解决了传统优化算法在处理大规模原油数据库时的局限性，也为炼油企业的原油采购与调和集成优化提供了新的思路和解决方案。

设计与实现:

在对原油数据库进行聚类任务时，经典高斯混合模型得到的聚类结果往往加剧了调和原油目标产率优化后的波动性。在极端情况下，这种波动性可能超过预设的可接受范围。经过深入分析，已确定该问题的根源在于原油价格数据维度与各蒸馏组分产率数据维度之间的相关性干扰。原油价格与馏分产率之间的相互作用会导致经典GMM算法的下聚类效果不佳。为了有效解决上述问题，本文提出了一种改进的GMM算法，该算法在EM算法的M步中加入了价格补偿函数，以提高GMM的聚类性能。这种改进方法的核心思想是利用原油价格数据与其他相关数据之间的互信息来修改原始的对数似然函数。通过这一改进策略，GMM算法可以更好地捕捉数据之间的复杂关系，从而获得更准确和稳定的聚类结果。改进的GMM算法的相关公式推导过程将简要概述如下：

1. 高斯混合模型的概率密度函数

GMM模型假设所有的n个数据点都是由k个高斯分布生成的，每个高斯分布称为一个成分。对于这k个高斯成分，每个成分的概率密度函数如方程（3.1）所示。

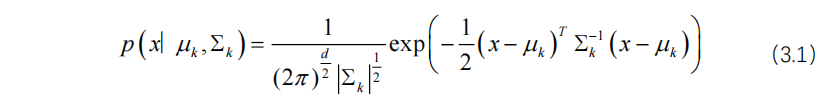
2. 潜变量与完整数据的对数似然函数

引入潜在变量，其中=1表示第i个数据点属于第j个高斯成分，而=0则表示不属于。包含潜在变量的完整数据的对数似然函数如式（3.2）所示。其中，表示第j个成分的权重，且所有成分的权重之和为1，即。

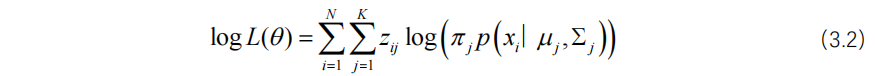
给定，对数似然函数（3.2）可以进一步简化为方程（3.3）：

当在EM算法中融入价格补偿函数时，方程（3.3）需要修改为方程（3.4）。其中，ρ为补偿因子，当原油价格较高且目标馏分产率也较高时，ρ取负值，且原油价格越高，ρ值越小；反之，当原油价格较高但目标馏分产率较低时，ρ取正值，且原油价格越高，ρ值越大。

3. E步：计算期望值

在E步中，根据当前参数估计值 和潜在变量的后验分布，计算完整数据对数似然的期望值，如方程（3.5）所示：

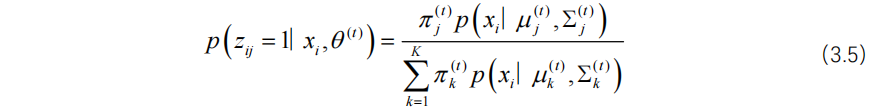
设该后验分布表示为。然后，按照方程（3.6）所示计算期望值：

引入一个期望公式，期望的计算可以简化为方程（3.7）：

4. M步：最大化期望

在EM算法中，在M步通过最大化Q(θ, θ^((t)))来更新参数θ，如方程（3.8）所示：

在M步中可以添加一个价格补偿函数，以选择与不完整数据密切相关的缺失数据，从而降低缺失数据的不确定性。假设X是与原油价格数据相关的离散随机变量，Z是与原油蒸馏馏分产率相关的离散随机变量，p(x,z)是它们的联合概率分布，p(x)和p(z)分别是它们的边缘概率分布。那么，价格补偿函数由方程（3.9）表示。在这里，条件熵H(X∣Z)用于量化在给定Z的条件下X的平均不确定性；而价格补偿函数PRC(X;Z)则衡量了Z对X不确定性的影响程度。如果Z与X之间不存在相关性，则价格补偿函数PRC(X;Z)的值为0。

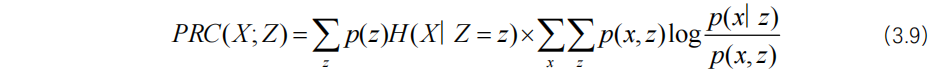
基于修改后的对数似然函数，即方程（3.4），方程（3.8）需要修改为方程（3.10）：

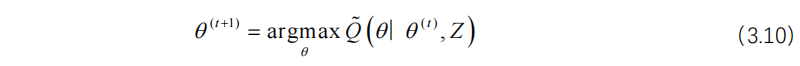
其中，的公式由方程（3.11）给出：

实验结果及分析:

为验证改进的高斯混合模型（GMM）算法在解决实际生产案例中的有效性，我们基于一个以燃料为导向的装置案例进行了仿真。以案例1的仿真结果为例，表1列出了基于聚类结果优化求解得到的调和原油性质。

Table 1. Properties of the blended crude oils in Case 1.

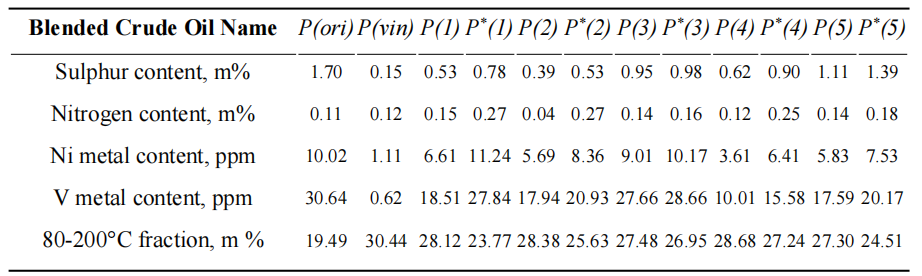
基于表1所示结果，使用改进GMM算法求解得到的调和原油性质与理想状态的差距明显小于使用经典GMM算法求解得到的数据，这表明使用改进GMM算法求解所得调和原油的性质更为稳定，变化范围更小。同时，使用改进GMM算法求解得到的目标馏分中调和原油的收率相较于初始产品的提升均高于使用经典GMM算法求解得到的结果，这表明使用改进GMM算法求解所得调和原油在目标蒸馏馏分中的收率提升更大，展现出更好的加工性能。

此外，为证明所提出的改进GMM算法能够解决原油采购与调和过程集成优化问题的挑战，本文分析了案例1-3中集成优化模型中的关键指标，详见表2。其中，Case1、2和3表示在直接基于初始原油数据库进行优化求解时的统计结果，而Case 1*、2*和3*则表示先使用改进GMM算法对原油数据库进行聚类再进行优化求解的结果。基于表2结果可知，使用改进GMM算法后，变量数量、约束数量以及求解时间均大幅减少。因此，本文提出的改进GMM算法解决了在大规模原油数据库下集成优化求解困难的问题。通过利用聚类算法对原油数据库进行初步筛选，可有效排除明显不可行的解，从而显著缩小了求解空间。

Table 2. Number of variables and constraints for Cases 1–3.

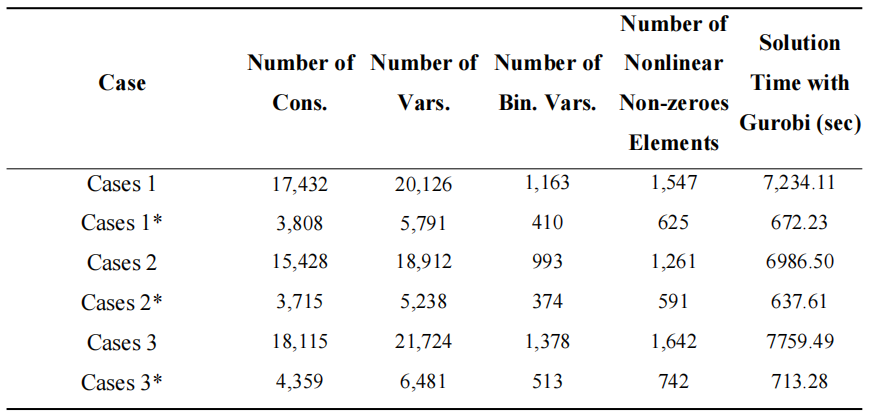
结论:

本文提出了一种改进的GMM算法，并将其应用于原油采购与调和调度的集成优化问题中。首先，通过在EM算法中添加价格补偿函数，提出了GMM算法的改进策略，以解决原油价格波动对聚类结果的干扰。通过实际案例验证了改进GMM算法在解决集成优化问题时的有效性。仿真结果表明，改进GMM算法能够有效缩小集成优化模型规模，解决了因原油种类过多而导致的集成优化问题求解难题。然而，改进GMM算法仍需人工设定K值，不合理的K值在很大程度上会影响聚类结果。因此，如何对原油数据进行有效处理，并通过结合深度学习的聚类算法实现更高精度的原油聚类，是未来工作的研究方向。

通讯作者简介:

高小永，人工智能学院副院长，教授，博士生导师，石大学者，校青年拔尖人才，自动化专业及控制科学与工程学科建设负责人，担任北京自动化学会常务理事、中国自动化学会过程控制专业委员会委员、中国自动化学会教育工作委员会委员、中国化工学会信息技术应用专业委员会副秘书长、中国系统工程学会过程系统工程专业委员会委员等。研究领域为复杂石油石化工业过程智能制造，主要方向有：机理与数据驱动的故障诊断、复杂工业过程建模与优化控制、工业过程计划与调度优化等。主持国家自然科学基金项目2项、北京市自然科学基金面上项目1项、校企联合项目30多项，发表SCI/EI等各类论文50多篇。

Email：x.gao@cqsbzx.com