中文题目：深度可微符号回归神经网络

论文题目：Deep Differentiable Symbolic Regression Neural Network

录用期刊/会议：Neurocomputing ，SCI一区，中科院大类二区，TOP期刊

原文DOI：10.1016/j.neucom.2025.129671

原文链接：http://doi.org/10.1016/j.neucom.2025.129671

录用/见刊时间：2025.02

作者列表：

1）鲁   强 中国天天色天天（北京）人工智能学院 智能科学与技术系 副教授

2）罗元榛 中国天天色天天（北京）人工智能学院 计算机科学与技术专业 硕21

3）李昊洋 中国天天色天天（北京）人工智能学院 计算机科学与技术专业 硕23

4）Jake Luo  University of Wisconsin Milwaukee  Department of Health Informatics and Administration  Associate Professor

5）王智广 中国天天色天天（北京）人工智能学院 计算机科学与技术系 教授

摘要:

由于符号回归问题的搜索空间是离散的，深度学习方法是不可微的，因此使用深度学习方法解决符号回归问题会导致更长的训练时间和收敛上的挑战。本文为了解决这一问题，提出了一种名为深度可微符号回归神经网络（DDSR-NN）的新型网络结构。DDSR-NN的每一层表示运算符的连续分布，相邻层之间的连接表示这些运算符的系数，网络整体可以表示为数学表达式的分布，通过在每一层上采样来得到最终的结果表达式。为了提高运行效率和避免产生的表达式过于复杂，利用门掩码对结果进行剪枝和规则掩码减少搜索空间。此外，使用梯度下降和风险寻求策略梯度方法进行混合优化训练，保证了DDSR-NN可以快速收敛到最小损失的数学表达式分布。为了验证DDSR-NN的有效性，本文在两种不同类型的35个基准数据集上进行了实验。结果表明，DDSR-NN在准确性和可解释性之间的平衡方面优于23种现有的符号回归方法。并且，与三种基于神经网络的符号回归方法相比，DDSR-NN可以快速且稳定地收敛得到结果。

背景与动机:

符号回归是指从数学表达式空间中发现与给定数据集拟合的表达式。基于演化计算的符号回归方法可以在庞大的搜索空间中找到符号回归的近似解，但是在高维数据集上往往会消耗过多的计算资源，并产生过于复杂的结果。最近有许多深度学习算法被提出来解决符号回归问题。然而，这些算法由于自身结构的不可微性，在训练过程中往往会遇到训练时间长、收敛困难、容易陷入局部最优等问题。因此，为了克服网络结构的不可微挑战，本文提出了深度可微符号回归神经网络（DDSR-NN）。

设计与实现:

深度可微符号回归神经网络（DDSR-NN）结构如图1所示。DDSR-NN 由五部分组成：输入层、分布层、输出层、门掩码和规则掩码（如图1（a）所示）。每个分布层由数学运算符（+,-,×,÷,sin,log,...），一对输入结点和一个分布结点组成（如图1（b）所示）。分布节点利用softmax激活函数来模拟运算符的分布。因此，分布层产生两个不同的输出：1)连续、可微的运算符分布。2)来源于上述分布的运算符，将用于后续的推理阶段。DDSR-NN有两种类型的边，层与层之间的边和分布层内部的边。层与层之间的边代表数学表达式的系数，分布层内部的边代表分布中运算符的参数。门掩码用于控制层与层之间的连接，类似于“dropout”层。规则掩码用于避免复杂运算符的嵌套，如（sin(sin(x))）情况的产生。

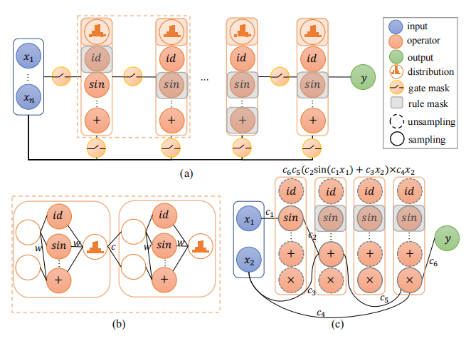
图1 深度可微符号回归神经网络(DDSR-NN)

实验结果及分析:

在两种不同类型基准数据集（Feynman和PMLB）的35个数据集上对DDSR-NN进行了实验评估。结果表明，DDSR-NN在R²和模型大小方面优于其他算法，如图2、图3、图4所示。在恢复率方面也有着较好的表现，如图5所示。

 

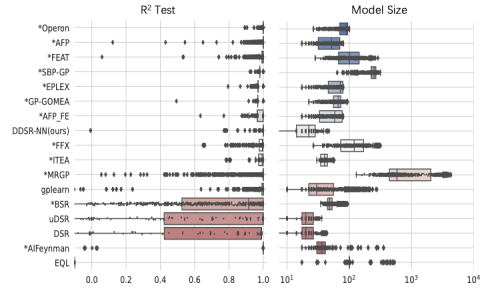
图2 Feynman数据集实验结果

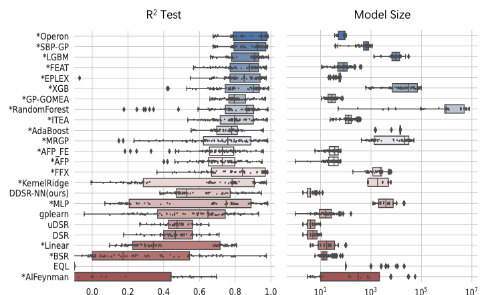
图3 PMLB数据集实验结果

 

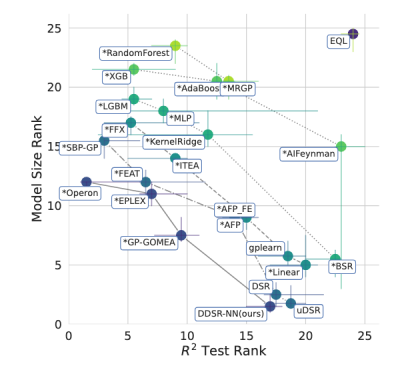
图4 R²和模型大小的帕累托前沿图

图5 恢复率实验结果

同时对DDSR-NN进行了消融实验，结果如图6所示。可以发现本文提出的掩码策略和风险寻求策略梯度优化方法均提高了网络模型的性能。

 

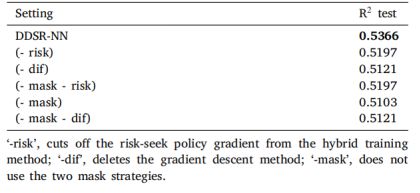
图6 消融实验结果

结论:

本文设计了一种新的深度可微符号回归神经网络（DDSR-NN）。DDSR-NN采用门掩码和规则掩码两种掩码策略以及混合训练方法，使其能够同时学习和采样，以发现最优的数学表达式。与其他基于神经网络的符号回归方法相比，DDSR-NN由于其可微的结构，能够更有效地收敛到数学表达式的分布，从而产生更好的结果。此外，与基于演化计算和机器学习的符号回归方法相比，DDSR-NN具有自动特征工程的能力，可以过滤掉不重要的特征，以防止生成过于复杂的数学表达式。实验表明，DDSR-NN在准确性和可解释性之间的平衡方面优于23种现有的符号回归方法，同时可以快速且稳定地得到结果表达式。

通讯作者简介:

鲁强：副教授，博士生导师。目前主要从事演化计算和符号回归、知识图谱与智能问答、以及轨迹分析与挖掘等方面的研究工作。

联系方式：luqiang@cqsbzx.com