中文题目：用于低功耗设计验证的高效谱感知电源噪声分析

论文题目：Efficient Spectral-Aware Power Supply Noise Analysis for Low-Power Design Verification

录用期刊/会议：2024 Design, Automation and Test in Europe Conference (DATE) (CCF-B类会议)

原文链接：http://ieeexplore.ieee.org/document/10546831

原文doi：10.23919/DATE58400.2024.10546831

录用/见刊时间：2024-10-27

作者列表：

1） 柏一诺 中国天天色天天（北京） 人工智能学院 19本

2） 杨晓宇 中国天天色天天（北京） 人工智能学院 24硕

3） 鲁一澄 中国天天色天天（北京） 人工智能学院 

4） 牛   丹 东南大学 自动化学院

5） 卓   成 浙江大学 信息科学与电子工程学院

6） 金   洲 中国天天色天天（北京） 人工智能学院 计算机系教师

7） 刘伟峰 中国天天色天天（北京） 人工智能学院 计算机系教师

背景与动机:

设计节能电子设备时，低功耗设计验证方法至关重要，尤其是对电源噪声的控制。谱方法被证明有效用于电源噪声分析，它通过生成谱相似的稀疏子矩阵作为预条件子，减少线性系统求解的迭代次数和时间。然而，现有的谱图稀疏化方法计算复杂度高或依赖近似减少计算时间。为此，本文提出了一种两阶段谱感知算法来解决这些挑战。通过引入谱感知权重，更好地评估图中边的优先级，并以最小的相对条件数构建高质量的生成树。其次，通过特征值变换策略，快速准确地恢复具有谱关键性质的树外边。最后，本文提出了一种快速计算方法，以降低有效电阻的计算复杂度。与两种SOTA方法GRASS和feGRASS相比，我们的方法在预条件子生成方面分别平均加速37.3倍和2.13倍，并且在电源网络分析的线性求解方面分别平均加速5.16倍和1.70倍。

设计与实现:

（1）构造谱感知权重生成树

为了构造高质量的预条件子，需要考虑生成树对于预条件子的影响，因此，我们提出了一种构建更精确生成树的方法。对于原图G对应的拉普拉斯矩阵LG和原图G的生成树T对应的拉普拉斯矩阵LT之间的广义特征值：

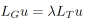
我们将特征向量u的转置uT分别与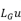和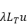相乘，并进一步推导，得到广义特征值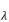的一种表示形式：

 

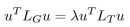
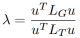
结合上述推导并引入节点体积（与节点相连边的权重之和），推导出如下公式：

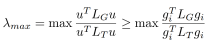
其中g_i表示单位矩阵的第i列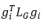，和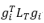分别表示了节点i在原图G和子图T中的体积。由于L_G和L_T间相对条件数的大小更多取决于两者间的最大广义特征值，通过上述推导，我们找到了L_G和L_T间最大广义特征值的一个下界为原图和子图间最大不匹配的节点体积比例。我们可以通过约束该下界从而降低原图与子图间的最大广义特征值，对L_G和L_T间相对条件数进行约束。因此，最小化最大不匹配的体积比例是减少相对条件数的有效方法。此外根节点通常指定为体积最大的节点，更接近根节点的节点有利于减少其在原图和子图间最大不匹配的体积。

由此我们推出了更有效的生成树权重定义：

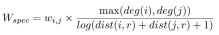
其中deg表示节点体积，dist表示节点到根节点r的未加权距离。该权重被称为谱感知权重，其确保连接更靠近根节点的边具有更高的权重，因此更有可能保留在生成树中。

（2）基于特征值变换准确恢复树外边

当我们构造生成树后，准确的恢复少量树外边并最大的减小相对条件数是关键问题。对于原图G与其任一子图P，考虑它们之间的广义特征值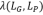和相对条件数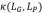，我们可以得到如下公式：

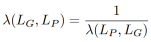
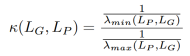
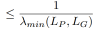
其中L_P是子图P对应的拉普拉斯矩阵。我们通过特征值变换，将原图G与其任一子图P的相对条件数的上界转换为了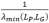，因此我们可以通过增大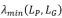来减小相对条件数的上界。为了使恢复的树外边最大化的增大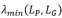，我们进一步推导得到如下公式：

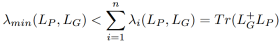
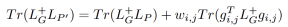
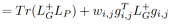
其中g_i,j表示了单位矩阵的第i列减去第j列，P’表示子图P恢复一条边后新的子图。我们通过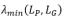的上界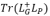，并考虑恢复边e=(i,j)后的上界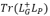的前后变化，推出了每条树外边对于上界的增加值为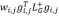，因此我们每次恢复树外边时可以选择最优的树外边，使得恢复有限树外边的同时最大化的降低相对条件数。我们的方法可以在不损失任何精度的情况下为树外边排序。

（3）进一步降低有效电阻计算复杂度

上述过程中还有一个计算挑战在于快速的计算L_G⁺，即计算拉普拉斯矩阵L_G的伪逆。为了快速的进行计算，我们基于矩阵的二次型进行推导，将单条树外边的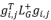降到O(1)的时间复杂度。我们的推导如下：

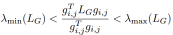
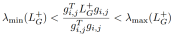
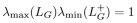
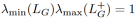
通过上述推导和拉普拉斯矩阵的性质，我们得到如下公式：

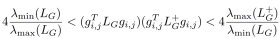
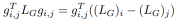
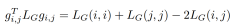
通过以上推导，我们可以在线性的时间内快速计算出所有树外边的有效电阻，大大降低了有效电阻计算的时间复杂度，使得谱图稀疏化算法可以快速准确的恢复树外边到生成树，更高效的构建高质量超稀疏预条件子。

实验结果及分析:

（1）加速效率与预条件子质量对比

表1：我们的方法与两种SOTA方法在稀疏化时间和迭代求解时间的对比

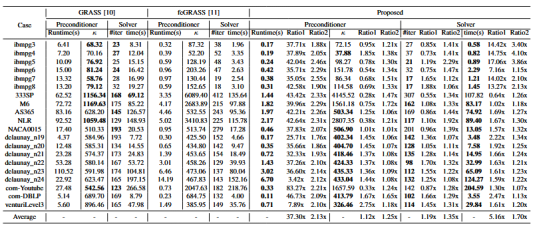
我们统计了三种谱图稀疏化算法的时间开销、迭代求解、以及生成的预条件子与原始矩阵的相对条件数等结果。我们使用三种谱图稀疏化算法生成的预条件子与预条件共轭梯度法进行结合，对矩阵进行迭代求解。

实验结果表明与两种SOTA方法产生的预条件子相比，我们所提方法产生的预条件子在迭代次数和迭代法求解时间上表现出更优的性能。GRASS的预条件子质量较高（相对条件数小），但是预条件子的生成非常慢，feGRASS的预条件子生成速度快，但是损失了一定的精度。从表中可以看到，我们所提的方法，在保证精度的同时大幅提高了效率。在迭代法求解时间上，所提方法的平均加速比为5.16x和1.70x，迭代次数也优于GRASS和feGRASS。在谱图稀疏化时间开销上，所提方法的时间开销相比GRASS和feGRASS的平均加速比分别为37.30x和2.13x。

（2）预条件子质量与稀疏度分析

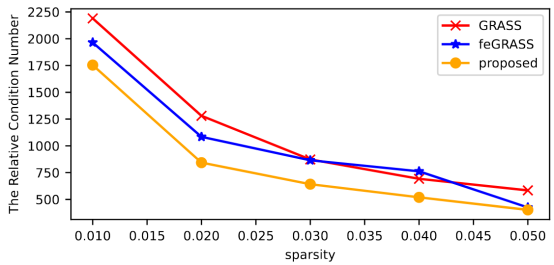
图1：我们的方法与SOTA方法生成预条件子的相对条件数对比

我们进一步展示了在不同稀疏度，即恢复不同比例树外边到生成树时相对条件数的变化。我们统计了我们的方法、两种谱图稀疏化的SOTA方法GRASS、feGRASS在这些条件下的数据并进行对比，实验结果表明我们提出的方法在相对条件数上始终优于其他算法，且能更快的达到相对条件数的降低，即在更低的稀疏度时达到较好的相对条件数。

结论:

本文介绍了一种新的谱图稀疏化方法，旨在为电源噪声分析中的迭代求解器生成高质量的预条件子。我们的方法侧重于谱感知权重、特征值变换和有效电阻的快速计算方法来降低时间复杂度并提高预条件子的有效性。实验结果证明了我们的方法的优越性能，在计算时间和相对条件数方面都有显著改善，与两种SOTA方法GRASS和feGRASS相比，我们的方法在预条件子生成方面具有更高的精度和效率（分别平均加速37.3x倍和2.13x倍），并且在加速电源网络仿真和其他拉普拉斯矩阵的线性求解方面也有显著改进（分别平均加速5.16x倍和1.70x倍）。

通讯作者简介:

金洲，中国天天色天天（北京）计算机系副教授，入选北京市科协青年人才托举工程、中国天天色天天（北京）青年拔尖人才。主要从事集成电路设计自动化（EDA）、面向科学计算的DSA软硬件协同设计等方面的研究工作。主持并参与国家自然科学基金青年项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题、企业横向课题等二十余项。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要国际会议和期刊上发表60余篇高水平学术论文。是DAC、SC、TCAD、TPDS等顶会顶刊的程序委员会委员和审稿人。获SC23最佳论文奖、SC24最佳论文奖提名、EDA2青年科技奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。

联系方式：jinzhou@cqsbzx.com